Integrated Phase along linefeed vs offset position.
sept 2004
A linefeed for the AO spherical dish (with Radius
R=870ft)
is placed R/2 feet below the center of curvature. Concentric rings
on the
dish focus energy at different places on the line feed. The edge of
the
dish focuses at the bottom of the line feed while points directly
below
the line feed (ignoring blockage) focus at the top of the line
feed.
The picture below is for a plane wave at the center of curvature of
the
dish. It shows the path for a ray of radius x feet from the center
of curvature.
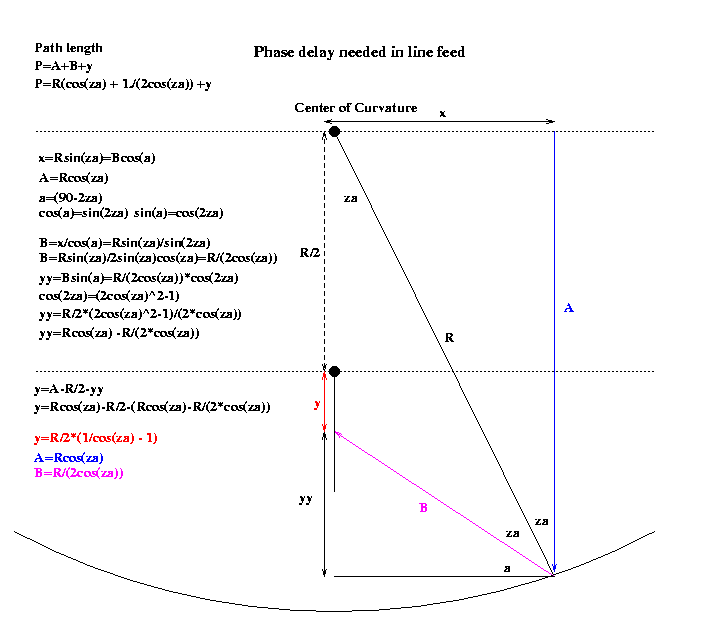
The ray goes along line A (blue),hits the dish,
reflects back along ray B (magenta), and then intersects the
line
feed a distance y (red line) from the paraxial point (R/2 feet below
the
center of curvature). The distance P=A+B+y must be a constant for
all values
of x along the plane wave. Remember that there is an axis of
symmetry so
x needs to be rotated (or integrated) around a ring of 360 degrees.
A summary of the computations are:
-
A=Rcos(za)
-
B=R/(2cos(za))
-
y=R/2 * (1./cos(za) - 1)
-
zamax=asin(500./870(radius)) = 35 degrees.
The plot
shows these relationships for the 1000ft (305m) ao dish (f/D=.5)
-
Fig top. Intersection of linefeed at position y versus
zenith angle
za.
-
Fig 2nd. Intersection of linefeed at position y versus
horizontal distance
x from center of curvature.
-
Fig 3rd. The integrated phase needed from a position y on the
linefeed
to y=0 so that a plane wave is brought to a focus at the
paraxial
surface. This distance is P-(A+B) (see above image). A ray
leaving
the center of curvature travels P=R+R/2 so P=1.5R. The plot has
y versus
(1.5R-(A+B)). This value is less than the physical distance, so
the phase
velocity of the wave guide must be greater than c.
-
Fig Bottom. The 3rd figure was the integral of the phase from
the y intersection
of the ray to y=0. This can be written as
phaseIntegral=integral(velC/velWG*dy) y=0
to
y
differentiating this with respect to y gives the c/waveGuide
velocity along the wave guide. This determines the taper you need
on the
wave guide to make things work. The taper starts with v=c at the
top and
goes down to about .4 (velWg=2.5c).
processing: x101/misc/linefeedphase.pro
home_~phil
