Horn positions, drift scan rotation angle.
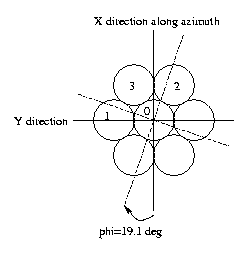 The
image on the left shows the 7 horns with the X axis along the azimuth arm.
To do drift scans, you need to rotate the feed array by an angle
phi so that the projected centers on the X axis are equi-spaced. You would
then place the azimuth at transit and let the sky drift by.
The
image on the left shows the 7 horns with the X axis along the azimuth arm.
To do drift scans, you need to rotate the feed array by an angle
phi so that the projected centers on the X axis are equi-spaced. You would
then place the azimuth at transit and let the sky drift by.
The beams on the sky are elliptical with the major
axis along the azimuth arm. The spatial sampling on the sky along the X
direction will be determined by the beam width (major axis) and the horn
spacing (projected onto the X axis). The spatial sampling along the Y direction
(ra) will be determined by the beam width (minor axis) and the temporal
sampling rate of the data.
Solving for the drift scan rotation angle phi.
Let S be the distance from horn 0 (H0) center to the center of any of the
other 6 horns. The starting horn angles are (the horns are spaced at 60
degree intervals):
H3 -30 degrees from X axis
H2 +30 degrees from the X axis
H1 0 degrees from the X axis
If we rotate the feed array by + phi degrees then the projection of
each horn center on the X axis is:
Px1= S*sin(phi)
Px2=S*cos(phi+30)
Px3=S*cos(phi-30)
The separation between the projected horn centers are:
Distance(Px1-Px0)=S*sin(phi)
Distance(Px2-Px1)=S*(cos(30+phi)-sin(phi)=S*(cos(30)cos(phi)-sin(30)sin(phi)-sin(phi))
Equating Distance(Px1-Px0) with (Px2-Px1) gives:
sin(phi)=cos(30)cos(phi)-1.5*sin(phi)
2.5*tan(phi)=cos(30)
phi=atan(cos(30)/2.5)=19.1066 degrees
The projections onto the Y axis after rotation are:
Py1=S*cos(phi)
Py2=S*sin(phi+30)
Py3=S*sin(phi-30)
The position and offsets in units S of the horn separation is then
(Positive Y is to the left to give a right handed system):
| |
Px,Py
(in units of horn separation S)
|
(Px,Py)
S=26 cm|
|
(Px,Py)
S=22cm
|
| Horn1 |
.327,.945 S |
(8.50,24.57) cm |
(7.19,20.79) cm |
| Horn2 |
.655,-.756 S |
(17.03,-19.66) cm |
(14.41,-16.63) cm |
| Horn3 |
.982,.189 S |
(25.53,4.91) cm |
(21.60,4.16) cm |
The plots show
the beam spacing for various horn separations:
Fig 1 Top: separation in arc seconds along the projected X axis versus
horn separation. The half beam width (216"/2) is over plotted in red.
To have the 3db point sit on the next beam requires a horn separation of
20.1 cm.
Fig 1 2nd: Beam spacing vs horn separation in units of .5*(FWHM) . A 26
cm horn separation is 1.3 times larger than the halfbeamwidth sampling.
Fig 1 3rd: This is the beam spacing the in the orthogonal direction versus
horn displacement.
Fig 1 bottom: This shows the time difference for the same RA to transit
in different horns.
These calculations have not taken into account all of the asymmetries
in the focal plane (e.g. X scale factor not constant).
processing: x101/mbeam/mbhorns/doit.pro
home_~phil
 The
image on the left shows the 7 horns with the X axis along the azimuth arm.
To do drift scans, you need to rotate the feed array by an angle
phi so that the projected centers on the X axis are equi-spaced. You would
then place the azimuth at transit and let the sky drift by.
The
image on the left shows the 7 horns with the X axis along the azimuth arm.
To do drift scans, you need to rotate the feed array by an angle
phi so that the projected centers on the X axis are equi-spaced. You would
then place the azimuth at transit and let the sky drift by.