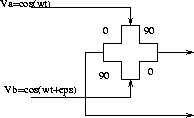
Terminology:
Va,Vb: Pol A,B voltages at the input to the hybrid.
Vaout,Vbout: Hybrid A,B voltage outputs.
eps : The relative phase
error between the two input signals.
w : Frequency
of the input signal.
The inputs signal at the two ports is then:
Va*cos(wt), Vb*cos(wt+eps)

When passing through the 90 deg phase delay, the cosine becomes a sine.
The voltage outputs from the hybrid are then:
To compute the power we time average the square of the voltage. When squaring, the cross terms sin(wt)cos(wt) average to zero (see above). The result is:
<Vaout2>=<cos(wt)2> * (Va-Vb*sin(eps))2
+ <sin(wt)2> * (Vb*cos(eps))2
<Vaout2>=.5(Va2+Vb2 *
sin(eps)2-2VaVb * sin(eps) + Vb2 * cos(eps)2)
<Vbout2>=<cos(wt)2> * (Vb*cos(eps))2
+ <sin(wt)2> * (Va+Vb*sin(eps))2
<Vbout2>=.5(Vb2*cos(eps)2 +
Va2 +2VaVbsin(eps)+Vb2*sin(eps)2)
<Vaout2>=.5(Va2 +Vb2 -
2VaVb*sin(eps))
<Vbout2) = .5(Va2 +Vb2
+ 2VaVb*sin(eps))
<Vbout2>-<Vaout2> = 2VaVb*sin(eps)
Let Rin = Va/Vb and <Rout2>=<Vaout2>
/ <Vbout2> then:
<Rout2> = (Rin2 + 1 - 2R*sin(eps))
/ (Rin2+1+2R*sin(eps)))
The first thing to notice is that if eps = 0, then the two outputs are equal, even if the input amplitudes vary.
The cal diodes used for calibration have been measured with the hybrid out. When the hybrid is switched in the routines will average the two cal values. This assumes that the hybrid has combined the two inputs with no phase errors. If two diodes are being used then there is no phase error since eps is not defined. When a single diode is used (correlated cal.. eg. the calibration button on the gui) then eps is defined and the output cal value in the two channels will vary depending on the phase error eps.
The figures show some examples.
The y axis is the power ratio of the hybrid outputs. The x axis is the phase error in degrees. The different colors show the values for different input power ratios. If you have a phase error of 20 degrees then the output power ratio will be a factor of two different (while the input power ratio was equal).
5 second cal on/offs were done at 1175,1300,1375, and 1415 Mhz using the correlator. The calDeflection/TsysDeflection is plotted versus frequency. Solid lines are polA and dashed lines are polB. The black lines are with the hybrid out. There is a difference in the two because the diodes are different. The red lines are the measured values with the hybrid in. The blue line is the expected value which is just the average of the two cal input values. Since there are two diodes, there is no phase error and the measured values lie quite close to the expected values.
This is the same measurement but now a single diode is split and then injected into both polarizations. The black lines are with the hybrid out. They differ by a small amount because the losses in the two lines are not equal. The blue is what we expect the hybrid to give: the average of the two inputs. The red lines show the values that are measured. They differ from the expected values by +/- 25%. Using the dual diodes, the system temperature for the two outputs is within 1K of each other so this difference is the cals and not Tsys.
The black lines show the measured cal values using a single diode and the hybrid. The blue line is what we expected them to be. The red lines are the computed values using a phase error of 16.4 degrees and an input amplitude ratio equal to the cal ratio measured when the hybrid was out. The agreement is excellent. The frequency dependence is because the 16.4 degree phase error was assumed to be caused by a path difference at 1415 Mhz. As you move to lower frequency this becomes a proportionally smaller phase error.The 16.4 degree phase error corresponds to 16.4/360*3e10/1415e6= .97 cm path difference. For a given frequency of observation you should be able to divide your wavelength into this length and then use the fraction of 360 deg as your phase error. Lookup the value in figure 1 to see what the ratio of the output powers will be.
Carl heiles measured a phase difference of 2.3 degrees between the cals at their injection point (the cal directional coupler). This means that the 16.4 +/- 2.3 degree error is between the cal injection point and the output of the 90 degree hybrid (it includes any hybrid errors).
f you are going to use the lwide system in circular mode and you aren't measuring polarized sources, then you should use 2 diodes (hcal) so that the system temperatures you compute are reasonable.
If you use lbw with the hybrid in and you are interested in polarization then you should probably use a single diode and use the cal measurement to straighten out how the polarization of your source has been screwed up by the hybrid. You won't be able to let the normal routines calibrate your data since the cal values will be wrong.
If you are a "real astronomer" (see C. heiles A heuristic intro to radioastronomical polarization, naic/nrao single dish workshop) then you would never use the hybrid to start with !!!
processing: x101/010703/doit.pro
plotting : x101/010703/doplot.pro
home_~phil